标签 笔记 下的文章
函数指针和指针函数
函数指针
- 函数指针是指向函数的指针变量,所以函数指针首先是指针变量,只不过他指向的是函数;
- C/CPP在编译时,默认分配给函数一个入口,该入口即是函数指针所要指向的地址,可以用为两个用途:
- 调用函数
- 做函数的参数
- 函数指针只能指向具有特定特征的函数,要求所有被同一指针所指向的函数必须具有相同的参数和返回值类型
- C语言标准的规定是函数指示符(即函数名)既不是左值也不是右值,但是CPP语言规定函数名属于左值,也就是说函数名转换为函数指针的右值属于左值向右值的转换
- 函数名除了可以作为
sizeof和取地址&的操作数,函数名在表达式中可以自动转换为函数指针类型的右值,所以通过一个函数指针调用所指向的函数,不需要在函数指针面前添加操作符号* - 指向函数的指针变量没有自增
++和 自减--操作
函数指针的声明形式:
返回类型 (*函数指针名称)(参数列表) -> C
返回类型 (类名称::*函数成员名称)(参数列表) -> CPP
这里借用 维基百科给出的样例
/* 例一:函数指针直接调用 */
# ifndef __cplusplus
# include <stdio.h>
# else
# include <cstdio>
# endif
int max(int x, int y)
{
return x > y ? x : y;
}
int main(void)
{
/* p 是函数指针 */
int (* p)(int, int) = & max; // &可以省略
// int (* p)(int, int) = max;//与上条语句等价
int a, b, c, d;
printf("please input 3 numbers:");
scanf("{2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}d {2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}d {2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}d", & a, & b, & c);
/* 与直接调用函数等价,d = max(max(a, b), c) */
d = p(p(a, b), c);
printf("the maxumum number is: {2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}d\n", d);
return 0;
}
/* 例二:函数指针作为参数 */
struct object
{
int data;
};
int object_compare(struct object * a,struct object * z)
{
return a->data < z->data ? 1 : 0;
}
struct object *maximum(struct object * begin,struct object * end,int (* compare)(struct object *, struct object *))
{
struct object * result = begin;
while(begin != end)
{
if(compare(result, begin))
{
result = begin;
}
++ begin;
}
return result;
}
int main(void)
{
struct object data[8] = {{0}, {1}, {2}, {3}, {4}, {5}, {6}, {7}};
struct object * max;
max = maximum(data + 0, data + 8, & object_compare);
return 0;
}
数据结构PTA笔记
网络与信息安全-数据结构作业1-数据结构基本概念
数据结构(逻辑结构 / 存储结构 / 数据的运算)
逻辑结构
- 数据的逻辑结构指的是数据元素之间的逻辑关系,就是从逻辑关系上描述数据,与数据的存储无关,独立于计算机的,数据的逻辑结构分为线性结构 和 非线性结构,线性表是典型的线性结构,集合/树/图是典型的非线性结构
- 集合结构中的数据元素之间仅有 属于同一集合的关系
- 线性结构中的数据元素之间仅存在 一对一 的关系
- 树形结构元素之间存在一对多关系,线性结构元素之间存在一对一关系,图形 / 网状结构元素之间存在多对多关系
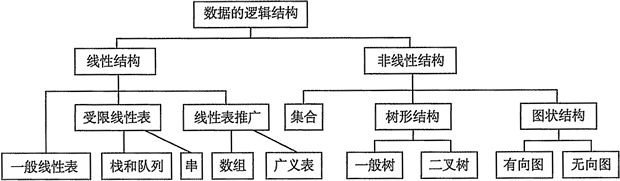
- 与数据元素本身的形式、内容、相对位置、个数无关的是数据的 (逻辑结构)
- 存储结构是对内容和个数的体现
- 存储实现是对内容的体现
- 运算实现是对形式的体现
- 逻辑实现是理论上虚拟的东西,与数据元素本身无关
- 常见的线性的数据结构: 线性表,栈,队列,双队列,数组,串
- 常见的非线性数据结构: 二维数组,多维数组,广义表,树(二叉树等),图,堆
存储结构
存储结构是指数据结构在计算机中的表示,也叫做物理结构。它包括数据元素的表示和关系的表示,是逻辑结构用计算机语言的实现。主要包括:顺序储存 / 链式储存 / 索引储存 / 散列储存。
- 顺序储存: 把逻辑上相邻的元素储存在物理位置上也相邻的地方,每一次都占用一整块内存单元
- 链式储存: 逻辑上相邻的元素在物理上不一定相邻,由指示元素储存地址的指针来表示元素之间的逻辑关系,可以不占用一整块的内存空间,但是由于使用了指示元素的指针,所以需要额外申请空间
- 索引储存: 在储存元素的同时,建立附加的索引表,一般形式是{关键字,元素}, 类似于CPP 的 map , 检索速度提高,但是空间增大,在增删元素时,耗时增加
- 散列储存: 根据元素的某一种性质直接计算出该元素出现的地址,类似于 Hash, 增删改元素快速,但是有可能出现碰撞的可能
数据的计算
数据结构 — — 并查集
并查集一般用于对动态连通性的判断,主要应用于判断两个不相交元素是否在同一个集合,两个点是否连通,变量名等同性以及间接好友的判断。同时并查集经常作为其他模板的一部分实现某些功能
并查集常用于的题型为判断某两个元素是否属于同一个集合,判断图是否连通或是否有环,或配合其他算法如最小生成树Kruskal,与DP共同使用等。
一般,并查集都会实现两种操作,就是查询函数,和链接函数。
普通并查集
类似于树,按照节点的方式来储存,理解并查集。其中的元素的储存,是由原始父节点为代表的树形结构。
每一个元素, 都是一个集合,其中的数值,指向 上层节点(父节点),由此方法我们可以推断,
只要两个节点所储存的最原始的父节点相同, 则两个点所代表的元素位于同一个集合。
路径压缩
为了进一步加快查找的速度,我们直接将新加入的节点,连接到原始节点上,这样就可以直接看出,两元素是否位于相同集合。
三个操作 (数组为例)
初始化操作
建立合适的储存方式,一般有结构体和数组两种,差别不大,功能是一样的。
基本的初始化,就是建立每一个节点的信息,比如 要储存当前元素的父节点,要储存当前元素在树内的深度,
当前元素所代表的数值意义等等。
有时可以将元素所代表的数值意义和当前元素的父节点合并表示,根据题目不同,还要建立别的,具体再分析。
#include <bits/stdc++.h>
const int maxn = 100000;
int m[maxn] = {0};
int r[maxn] = {0};// 数据比较多,节点链比较长时,合并短的,节约时间。
void init(int End)
{
for(int i = 0;i < maxn && i <= End; i++)//初始化每一个节点都是父节点,深度为0
{
m[i] = i;
r[m] = 0;
}
return;
}
查找操作
- 普通并查集的基本查找代码比较简单,这里直接给出代码。
int Find(int i)
{
if(m[i] == i)
return i;
else
return m[i] = Find(m[i]);//路径压缩
}
- 补充循环+路径压缩的代码 2018-05-20
int Find(int i)
{
int pi = i;
while(pre[pi] != pi)
pi = pre[pi]; // 找到根节点
int si = i,j;
while(si != pi)
{
j = pre[si]; // 记录当前节点的前导节点
pre[si] = pi;// 当前节点的前导节点设置为根节点
i = j;// 继续处理当前节点的前导节点的前导节点为根节点
}
return pi;
}
合并操作
- 先给出不考虑深度(单链长度) 的代码
void Union(int a,int b){
m[Find(b)] = Find(a);
return;
}
下面是考虑深度(单链长度) 的代码
void Union(int i,int j)
{
i=Find(i);
j=Find(j);
if(i == j)
return ;
if(rank[i] > rank[j])
set[j] = i;
else
{
if(rank[i] == rank[j])
rank[j]++;
set[i] = j;
}
}
SDUSTOJ:Problem D: 儿童绘画游戏
山东科技大学的一道 OJ 题目
