分类 数据结构 下的文章
7-1 jmu-ds-集合的并交差运算 (15 分)- 很神奇的一道题目
这么久没遇到过这样的题目了,忍不住写一下~
题目链接:PTA
7-1 jmu-ds-集合的并交差运算 (15 分)
/*
有两个整数集合A和B,现在要求实现集合的并、交、差运算。
例如A={2,7,9} ,B={3,7,12,2}, 则集合的并C=A∪B={2,7,9,3,12},
而集合的交 C=A∩B={2,7},集合的差C=A-B={9}。
集合A和B中元素个数在1~100之间。
输入格式: 三行,
第一行分别为集合A,B的个数
第二行为A集合的数据
第三行为B集合的数据
输出格式: 三行
第一行集合并的结果:C的个数及C中的元素
第二行集合交的结果:C的个数及C中的元素
第三行集合差的结果:C的个数及C中的元素
输出结果以元素在A集合中的先后顺序输出,不能改变数据的输出顺序
输入样例: 3 4 2 7 9 3 7 12 2
输出样例: 5 2 7 9 3 12 2 2 7 1 9
*/
这个题意很简单,一开始没注意到顺序的问题,使用的set 的函数来进行,错了,后来发现了顺序的问题,改了改再去提交还是不对,这个时候我看到了通过率 是 0 %,就觉得肯定后台数据有问题,就一直放着没做,结果就考试结束了 直到今天2018/09/25,
我一定要记住这个日子,因为这个题目在我百度谷歌都无果后,终于知道了正确答案~,说出来我自己都不信
你只要,在输出集合的时候,当集合中元素,小于5 或者 6 的时候,不输出个数就行了。。
此处感谢软件的机智勇敢大无畏的同学们,是你们让我知道了,这道题的正确解答是什么,死的明明白白
#include <bits/stdc++.h>
using namespace std;
typedef int ElemType;
typedef struct
{
ElemType *elem;
int length;
int listsize;
} SqList;
void Sqlistiniti(SqList &s)
{
s.elem = new ElemType[1009];
s.length = 0;
s.listsize = 1009;
}
void Sqlistcreate(SqList &s, int n)
{
Sqlistiniti(s);
s.length = n;
for (int i = 0; i < n; i++)
{
cin >> s.elem[i];
}
}
SqList bingji(SqList &a, SqList &b)
{
SqList c;
Sqlistiniti(c);
int i;
int k;
for (i = 0; i < a.length; i++)
{
c.elem[i] = a.elem[i];
c.length++;
}
int n = i;
for (int j = 0; j < b.length; j++)
{
int flag = 1;
for (k = 0; k < c.length; k++)
{
if (b.elem[j] == c.elem[k])
{
flag = 0;
break;
}
}
if (flag)
{
c.elem[i++] = b.elem[j];
c.length++;
}
}
return c;
}
SqList jiaoji(SqList &a, SqList &b)
{
SqList c;
Sqlistiniti(c);
int k = 0;
for (int i = 0; i < a.length; i++)
{
for (int j = 0; j < b.length; j++)
{
if (a.elem[i] == b.elem[j])
{
c.elem[k++] = a.elem[i];
c.length++;
}
}
}
return c;
}
SqList chaji(SqList &a, SqList &b)
{
SqList c;
Sqlistiniti(c);
int j, k = 0;
for (int i = 0; i < a.length; i++)
{
int flag = 1;
for (j = 0; j < b.length; j++)
{
if (a.elem[i] == b.elem[j])
{
flag = 0;
break;
}
}
if (flag)
{
c.elem[k++] = a.elem[i];
c.length++;
}
}
return c;
}
void Sqlistprint(SqList &s, SqList &a)
{
int f = 0;
if (a.length <= 6)
{
cout << s.length;
for (int i = 0; i < s.length; i++)
{
cout << " " << s.elem[i];
}
}
else
for (int i = 0; i < s.length; i++)
{
if (i)
cout << " ";
cout << s.elem[i];
}
cout << endl;
}
int main()
{
SqList a, b, c;
int n1, n2;
cin >> n1 >> n2;
Sqlistcreate(a, n1);
Sqlistcreate(b, n2);
c = bingji(a, b);
Sqlistprint(c, a);
c = jiaoji(a, b);
Sqlistprint(c, a);
c = chaji(a, b);
Sqlistprint(c, a);
return 0;
}
数据结构PTA笔记
网络与信息安全-数据结构作业1-数据结构基本概念
数据结构(逻辑结构 / 存储结构 / 数据的运算)
逻辑结构
- 数据的逻辑结构指的是数据元素之间的逻辑关系,就是从逻辑关系上描述数据,与数据的存储无关,独立于计算机的,数据的逻辑结构分为线性结构 和 非线性结构,线性表是典型的线性结构,集合/树/图是典型的非线性结构
- 集合结构中的数据元素之间仅有 属于同一集合的关系
- 线性结构中的数据元素之间仅存在 一对一 的关系
- 树形结构元素之间存在一对多关系,线性结构元素之间存在一对一关系,图形 / 网状结构元素之间存在多对多关系
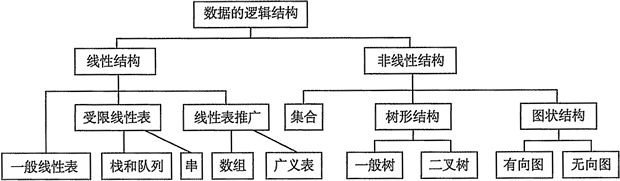
- 与数据元素本身的形式、内容、相对位置、个数无关的是数据的 (逻辑结构)
- 存储结构是对内容和个数的体现
- 存储实现是对内容的体现
- 运算实现是对形式的体现
- 逻辑实现是理论上虚拟的东西,与数据元素本身无关
- 常见的线性的数据结构: 线性表,栈,队列,双队列,数组,串
- 常见的非线性数据结构: 二维数组,多维数组,广义表,树(二叉树等),图,堆
存储结构
存储结构是指数据结构在计算机中的表示,也叫做物理结构。它包括数据元素的表示和关系的表示,是逻辑结构用计算机语言的实现。主要包括:顺序储存 / 链式储存 / 索引储存 / 散列储存。
- 顺序储存: 把逻辑上相邻的元素储存在物理位置上也相邻的地方,每一次都占用一整块内存单元
- 链式储存: 逻辑上相邻的元素在物理上不一定相邻,由指示元素储存地址的指针来表示元素之间的逻辑关系,可以不占用一整块的内存空间,但是由于使用了指示元素的指针,所以需要额外申请空间
- 索引储存: 在储存元素的同时,建立附加的索引表,一般形式是{关键字,元素}, 类似于CPP 的 map , 检索速度提高,但是空间增大,在增删元素时,耗时增加
- 散列储存: 根据元素的某一种性质直接计算出该元素出现的地址,类似于 Hash, 增删改元素快速,但是有可能出现碰撞的可能
数据的计算
[PTA] 6-1 顺序表基本操作(10 分)
题目来自 网络与信息安全-数据结构作业1-数据结构基本概念 6-1
原题描述
6-1 顺序表基本操作(10 分)
本题要求实现顺序表元素的增、删、查找以及顺序表输出共4个基本操作函数。L是一个顺序表,函数Status ListInsert_Sq(SqList &L, int pos, ElemType e)是在顺序表的pos位置插入一个元素e(pos应该从1开始),函数Status ListDelete_Sq(SqList &L, int pos, ElemType &e)是删除顺序表的pos位置的元素并用引用型参数e带回(pos应该从1开始),函数int ListLocate_Sq(SqList L, ElemType e)是查询元素e在顺序表的位次并返回(如有多个取第一个位置,返回的是位次,从1开始,不存在则返回0),函数void ListPrint_Sq(SqList L)是输出顺序表元素。实现时需考虑表满扩容的问题。
函数接口定义:
Status ListInsert_Sq(SqList &L, int pos, ElemType e);
Status ListDelete_Sq(SqList &L, int pos, ElemType &e);
int ListLocate_Sq(SqList L, ElemType e);
void ListPrint_Sq(SqList L);
其中 L 是顺序表。 pos 是位置; e 代表元素。当插入与删除操作中的pos参数非法时,函数返回ERROR,否则返回OK。
裁判测试程序样例:
//库函数头文件包含
#include
#include
#include
//函数状态码定义
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;
//顺序表的存储结构定义
#define LIST_INIT_SIZE 100
#define LISTINCREMENT 10
typedef int ElemType; //假设线性表中的元素均为整型
typedef struct{
ElemType* elem; //存储空间基地址
int length; //表中元素的个数
int listsize; //表容量大小
}SqList; //顺序表类型定义
Status ListInsert_Sq(SqList &L, int pos, ElemType e);
Status ListDelete_Sq(SqList &L, int pos, ElemType &e);
int ListLocate_Sq(SqList L, ElemType e);
void ListPrint_Sq(SqList L);
//结构初始化与销毁操作
Status InitList_Sq(SqList &L){
//初始化L为一个空的有序顺序表
L.elem=(ElemType *)malloc(LIST_INIT_SIZE*sizeof(ElemType));
if(!L.elem)exit(OVERFLOW);
L.listsize=LIST_INIT_SIZE;
L.length=0;
return OK;
}
int main() {
SqList L;
if(InitList_Sq(L)!= OK) {
printf("InitList_Sq: 初始化失败!!!n");
return -1;
}
for(int i = 1; i <= 10; ++ i)
ListInsert_Sq(L, i, i);
int operationNumber; //操作次数
scanf("{2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}d", &operationNumber);
while(operationNumber != 0) {
int operationType; //操作种类
scanf("{2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}d", & operationType);
if(operationType == 1) { //增加操作
int pos, elem;
scanf("{2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}d{2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}d", &pos, &elem);
ListInsert_Sq(L, pos, elem);
} else if(operationType == 2) { //删除操作
int pos; ElemType elem;
scanf("{2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}d", &pos);
ListDelete_Sq(L, pos, elem);
printf("{2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}dn", elem);
} else if(operationType == 3) { //查找定位操作
ElemType elem;
scanf("{2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}d", &elem);
int pos = ListLocate_Sq(L, elem);
if(pos >= 1 && pos <= L.length)
printf("{2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}dn", pos);
else
printf("NOT FIND!n");
} else if(operationType == 4) { //输出操作
ListPrint_Sq(L);
}
operationNumber--;
}
return 0;
}
/* 请在这里填写答案 */
输入格式: 第一行输入一个整数operationNumber,表示操作数,接下来operationNumber行,每行表示一个操作信息(含“操作种类编号 操作内容”)。 编号为1表示插入操作,后面两个参数表示插入的位置和插入的元素值 编号为2表示删除操作,后面一个参数表示删除的位置 编号为3表示查找操作,后面一个参数表示查找的值 编号为4表示顺序表输出操作 输出格式: 对于操作2,输出删除的元素的值 对于操作3,输出该元素的位置,如果不存在该元素,输出“NOT FOUND”; 对于操作4,顺序输出整个顺序表的元素,两个元素之间用空格隔开,最后一个元素后面没有空格。
输入样例:
4
1 1 11
2 2
3 3
4
输出样例:
1
3
11 2 3 4 5 6 7 8 9 10
笔记部分
一、 realoc 函数
realloc 函数的使用要求引入头文件
stdlib.h该函数的原型为realloc(void *__ptr, size_t __size)
void* __cdecl realloc(
_Pre_maybenull_ _Post_invalid_ void* _Block,
_In_ _CRT_GUARDOVERFLOW size_t _Size
);
- 也就是传入的第一个参数是指针类型,第二个参数是更改后的大小。
- 如果操作使得内存分配减少,那么函数仅仅是改变了索引信息;
- 如果操作使得内存分配增加,那么当当前内存之后有足够的内存来扩展的时候,函数直接扩展内存,返回指针;当当前内存段之后没有足够的空闲内存时,函数寻找堆 中的第一个能满足申请内存大小的内存段,将数据复制,并且释放旧的内存,返回指针。申请失败返回NULL
- 返回的是指针,但无论何种情况,实际上都不保证返回原指针(可以通过输出地址尝试),原指针会被函数自动的释放,不可二次释放原指针
AC 代码
void ListPrint_Sq(SqList L){
ElemType maxn = L.length;
for (ElemType i = 0; i < maxn; ++i){
if(i){
printf(" ");
}
printf("{2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}d", L.elem[i]);
}
puts("");
return;
}
int ListLocate_Sq(SqList L, ElemType e){
ElemType maxn = L.length;
for (ElemType i = 0; i < maxn; ++i){
if(L.elem[i] == e){
return i + 1;
}
}
return FALSE;
}
Status ListDelete_Sq(SqList &L, int pos, ElemType &e){
ElemType maxn = L.length;
if(pos < 1 || pos > maxn){
return ERROR;
}
e = L.elem[pos - 1];
for (ElemType i = pos - 1; i < maxn - 1; ++i){
L.elem[i] = L.elem[i + 1];
}
L.length -= 1;
// printf("DEL {2186e5f7970dac0e9cf7cfc7913f086a2d003118a30b627bce447294ada8be4e}dn", L.length);
// ListPrint_Sq(L);
return OK;
}
Status ListInsert_Sq(SqList &L, int pos, ElemType e){
ElemType maxn = L.length;
if(pos < 1 || pos > maxn + 1){
return ERROR;
}
if(L.length >= L.listsize){
ElemType *newe;
newe = (ElemType *)realloc(L.elem, (L.listsize + LISTINCREMENT) * sizeof(ElemType));
if(!newe){
return OVERFLOW;
}
else {
L.elem = newe;
L.listsize += LISTINCREMENT;
}
}
for (ElemType i = maxn; i >= pos; --i){
L.elem[i] = L.elem[i - 1];
}
L.elem[pos - 1] = e;
L.length += 1;
// ListPrint_Sq(L);
return OK;
}
/*
11 1 2 3 4 5 6 7 8 9 10
11 2 3 4 5 6 7 8 9 10
*/
数据结构 — — 树状数组
title:
date: 2018-05-20 12:54:17
tags: [树状数组,数据结构,算法]
定义
树状数组也叫做Fenwick树, 也叫做 Binary Indexed Tree,经常被用来 高效的计算数列的前缀和 和 区间和等 查询和修改的时间复杂度皆为O(log(n)),空间复杂度为O(n);
