title:
date: 2018-05-20 12:54:17

tags: [树状数组,数据结构,算法]

定义

树状数组也叫做Fenwick树， 也叫做 Binary Indexed Tree，经常被用来 高效的计算数列的前缀和 和 区间和等 查询和修改的时间复杂度皆为O(log(n)),空间复杂度为O(n);

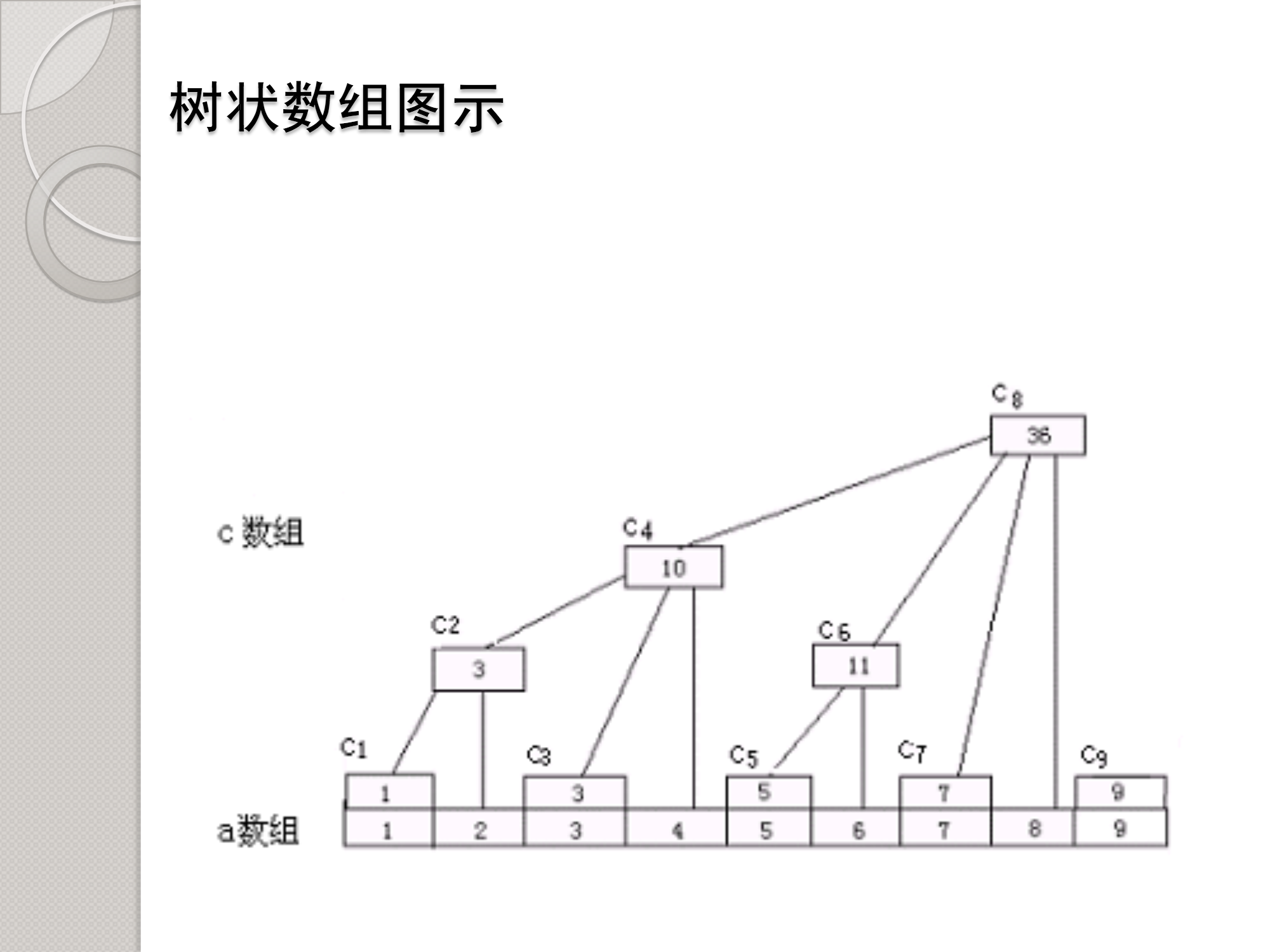
图片源自banananana:herf
图片中的a 是原数据数组，c 是树状数组，不难发现

C1 = A1
C2 = A1+A2
C3 = A3
C4 = A1+A2+A3+A4
C5 = A5
C6 = A5+A6
C7 = A7
C8 = A1+A2+A3+A4+A5+A6+A7+A8

原理及几个操作函数

lowbit()

int lowbit(int x)
    return (x & -x);

此函数利用的是二进制的性质，来求得某一个数字的从后往前的连续0的位数，也就是取出数字最低位的1.

举例说明：
-x 代表 x 的负数 计算机中负数使用对应的 正数的补码 来表示.
对于数字 6，其二进制为110，-x 就是 010,进行求与运算结果为 0010 = 2^1 = 2；

按照此方法求得的答案k，用原来的 x 加上k，就得到了此节点的父节点，而如果将原来的 x 减去k，就得到了此节点的上一个父节点。

单点修改-change()

// 将a数组里的第x个元素更改d,数组向后更新
void change(LL& a,int x,int d){
    if(x < 1)
        return ;
    while(x < maxn){
        a[x] += d;
        x += lowbit(x);
    }
}

求和函数-addsum()

// 数组向前求和
LL addsum(LL& a,int l){
    LL ans = 0;
    while(l > 0){
        ans += a[l];
        l -= lowbit(l);
    }
    return ans;
}

区间更新 + 区间查询

观察下列式子：

a[1] + a[2] + ... + a[n] = (c[1]) + (c[1]+c[2]) + ... + (c[1]+c[2]+...+c[n])

= n * c[1] + (n-1) * c[2] + ... + c[n]

= n * (c[1] + c[2] + ... + c[n]) - (0 * c[1] + 1 * c[2] + ... + (n-1) * c[n]) (①)

那么我们就维护一个数组c2[n]，其中c2[i] = (i - 1) * c[i]
每当修改c的时候，就同步修改一下c2，这样复杂度就不会改变
那么可得 ① = n * addsum(c,n) - addsum(c2,n);

例子

POJ // Code 用 树状数组 给出
CodeVS

先给出代码：

#include <bits/stdc++.h>

using namespace std;
typedef long long LL;

const int maxn = 1e5 + 10;

LL a[maxn + 10] = {0};
LL m[maxn + 10] = {0};
LL m1[maxn + 10] = {0};

LL lowbit(LL x)
{
    return (x & -x);
}

LL change(LL* s, LL n, LL d)
{
    if (n < 1)
        return 0;
    while (n < maxn)
    {
        s[n] += d;
        n += lowbit(n);
    }
    return 1;
}

LL addsum(LL* s, LL x)
{
    LL ans = 0;
    while (x > 0)
    {
        ans += s[x];
        x -= lowbit(x);
    }
    return ans;
}

int main()
{
    std::ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    LL N, Q;
    while (cin >> N >> Q)
    {
        memset(m, 0, sizeof(m));
        for (LL i = 1; i <= N; i++)
        {
            cin >> a[i];
            change(m, i, a[i] - a[i - 1]);
            change(m1, i, (i - 1) * (a[i] - a[i - 1]));
        }
        char C;
        LL a, b, c;
        while (Q--)
        {
            cin >> C;
            if (C == 'Q')
            {
                cin >> a >> b;
                LL sumo = (a - 1) * addsum(m, a - 1) - addsum(m1, a - 1);
                LL sumt = b * addsum(m, b) - addsum(m1, b);
                cout << sumt - sumo << endl;
            }
            else
            {
                cin >> a >> b >> c;
                change(m, a , c);
                change(m, b + 1, -c);
                change(m1, a, (a - 1) * c);
                change(m1, b + 1, -c * (b));
            }
        }
    }
    return 0;
}

• 当用户输入数据的时候，每一次更新，先将树状数组 m 从 a 之后更新为加上 c，然后为了保证区间更新，再将树状数组 m 的b + 1之后再减去 c，如此，就保证了区间更新。
• 区间更新的同时，要更新树状数组 m1， 从a 位开始都加上 (a-1) * c, 从 b + 1位开始，都减去 c * b, 就保证了第二个数组是在 logn 的基础上更新的，保证了时间。
• 区间的查询，我们只需要取出m 数组的a - 1位乘上( a - 1 )再减去m1 的a - 1 的a - 1的查询，得到前a 项的前n 项和， 再减去类似方法求出的前 b 项的前 n 项和即可得到所求区间的和！